A. Bows, bouncing and the centre of percussion
So far, we have talked a lot about bowing but we haven’t actually included a real violin bow in the discussion: the computer simulations have assumed a rigid “bow” acting at a single point on the string, or at several points to represent the finite width of the ribbon of bow hair. We now look to see what different issues might arise when a conventional violin bow is used in place of a rigid rod.
First, we need to understand the anatomy of bows. A carefully-shaped stick, usually made from a wood called pernambuco, has a cranked tip carved into it. This tip carries one end of the ribbon of bow-hair. The other end is carried by the “frog”, a block of wood (usually) which can slide along the stick, secured by a threaded screw within the stick which can be used to tension the hair. In violin bows of professional standard, the ribbon consists of 150—200 strands of horsehair, in a band approximately 10 mm wide.
The key figure in the development of the modern violin bow was François Tourte, working in France in the late 1780s. Before Tourte, bows for stringed instruments usually had a slight upward curve in the stick. Tourte reversed this, introducing the down-curved stick we see today. You can see a typical modern bow compared to an earlier bow (a treble viol bow) in Fig. 1. Figure 2 shows a close-up of the two bow tips.


An important consequence of the downward curvature of the bow stick was highlighted by Askenfelt and Guettler [1]: the Tourte form allows significantly higher tension in the bow hair. As the hair is shortened, the tension tends to rotate the tip, and thus bend the stick upwards. If the curvature of the stick is already upwards, this extra curvature tends to make the stick less able to resist the axial force of the hair tension. But the Tourte stick gets straighter, not more curved, as the hair tension is increased within the usual working range.
Players are in no doubt that the bow is an important thing in its own right. They will have definite preferences for particular bows, and they may be prepared to spend a surprisingly large amount of money on a bow: a significant fraction of the value of the instrument itself. The physics behind this influence of the bow has proved quite elusive to understand. Some things are known, but if anything the question of preferences between bows remains even more mysterious than the corresponding question about preferences between violins (or cellos, or whatever). There are several possible ways that the bow can influence the sound and playing “feel” of a violin, and I will talk about two of them.
An expert violinist requires their bow to perform all kinds of sophisticated tricks, and my first category of physical attributes of a bow contains things which affect how the bow “feels in the hand”, and which thus contribute to the ease (or otherwise) of performing these tricks. If you hold a violin bow in the normal way, then wave it around in the air in the plane of the bow, elementary mechanics tells us that just three parameters are enough to determine how it will feel and behave. One of them is the total mass, and the other two are determined by how that mass is distributed: the stick is tapered, and it has additional mass near the ends in the form of the frog and the tip.
We could use various possible parameters to characterise this mass distribution, but there are two particular ones that are commonly used by bow-makers. First, and most intuitive, is the balance point (or “centre of mass”). The second parameter is something called the “centre of percussion”, and as well as completing our characterisation of the mass distribution it also relates to an important aspect of performance with a bow. Some kinds of bowing make use of the way the bow can rebound from the string. Examples are the bowing styles known as ricochet, spiccato and sautillé. You can see demonstrations of these, and many other kinds of bowing, in this YouTube video: go to the times 0:20 for ricochet, and 1:51 for spiccato-sautillé.
The definition of the centre of percussion goes like this. Imagine hanging the bow from the point marked “pivot” in Fig. 3: it is the position where the player will usually place their thumb when holding the bow in the normal way for classical music. Now think of tapping the bow-hair with a pencil. If you tap at a position close to the pivot, there will be a reaction force at the pivot, and it will be in the opposite direction to your tap. But if you tapped right at the other end, near the tip, the reaction force would be in the same direction as your tap, because it has to restrain the bow from rotating about somewhere near the middle. Somewhere in between these two tapping positions, there will be one particular place where there is no reaction force at all. This is the “centre of percussion”. It is marked with a green arrow in Fig. 3: it is about 2/3 of the way down the bow from the pivot point. The next link gives some technical details about all this.

Another way to describe the effect would be to think of lying the bow on its side on an ice rink so that it could slide around any way it wanted, and then tapping the hair in a horizontal direction with your pencil. When you tap exactly at the centre of percussion, the bow will start to move by rotating about the “pivot” point, even though there is no pivot present this time. If you tap anywhere else, the “pivot” point will move: in one direction if you are closer to the frog, and in the opposite direction if you are further from the frog.
When a player wants to perform ricochet or spiccato notes, they need the natural bouncing behaviour of the bow to do some of the work for them. This in turn depends on the position of the bowing point along the bow, partly through the influence of the centre of percussion. It seems reasonable that very rapid ricochet playing might be easier if the bowing point is fairly near the centre of percussion, so that the bow naturally wants to rotate around the player’s thumb during the bouncing action. Askenfelt and Guettler did an interesting study of “the perfect spiccato” [2], and they suggest that such strokes are “always played well inside the centre of percussion (about 10 cm)”. For the bow in Fig. 3, that position would lie halfway between the balance point and the centre of percussion. They also point out that such bowing techniques only became possible with the higher hair tension available from a Tourte bow. Viol players do not do such flashy bowings!
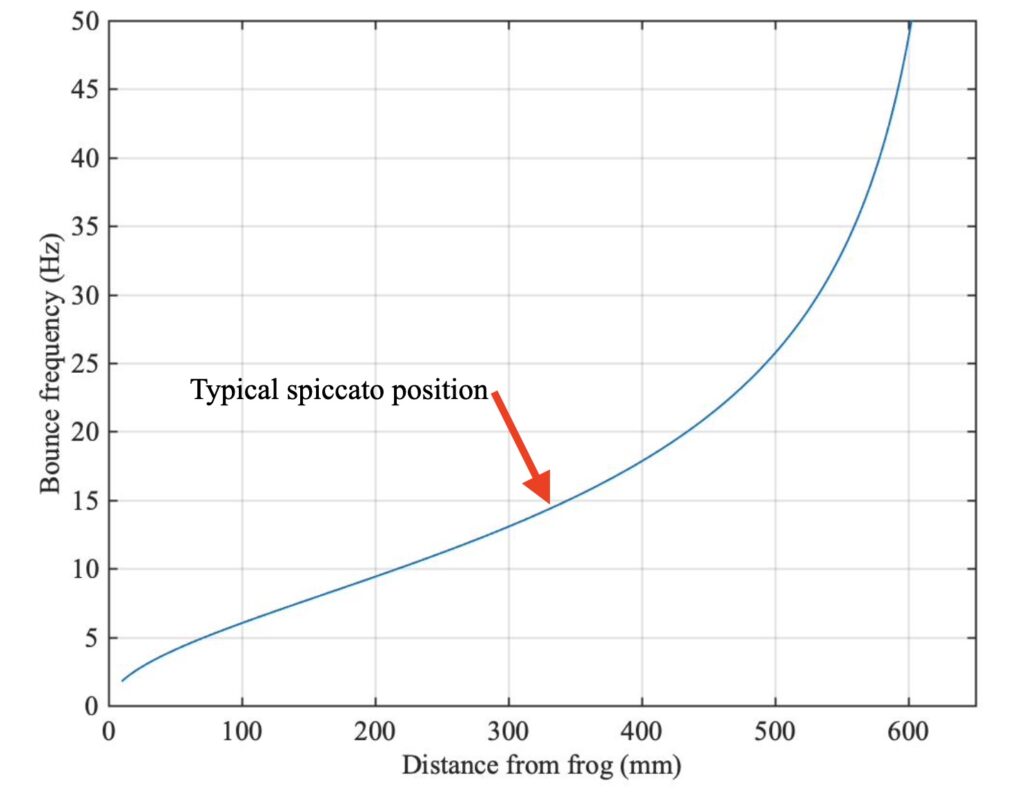
There is another aspect of the dynamics of a bouncing bow that is very important for a player aiming to perform rapid spiccato or ricochet. When the bow is in contact with a string, it has a resonant bouncing frequency determined by the inertia of the bow and a stiffness coming mainly from the bow-hair tension. This resonance frequency varies strongly with position along the bow, and also with bow-hair tension. Askenfelt and Guettler [1] gave a simplified theoretical expression for this: Fig. 4 shows a version of their plot. The next link describes their model. They tested a professional violinist with a wide variety of bows, asking them to play the same rapid spiccato with each one. They found that the player did indeed adjust the hair tension and bowing point for each bow so as to create essentially the same bouncing frequency every time.
B. Vibration of the bow stick and hair
We turn to another category of physical effects associated with a bow: things connected with vibration of the bow-stick and bow-hair. Now we enter a world of smoke and mirrors: many players and bow-makers have a deeply-held belief that the bow has a direct influence on the tone of a violin (not just on the ease of performing tricky bowings). But in fact there is at present very little hard evidence for how such an influence on tone might arise.
Of course the stick and hair of a bow can vibrate in various ways: the stick can show bending and twisting behaviour, while the hair is rather similar to a string, and can show transverse and longitudinal vibration. When these things are all coupled together, quite a range of vibration resonances can arise. But a bow, like a string, is very thin compared to the wavelength of sound, so it can make very little radiated sound in its own right. Any influence must, surely, come through interaction with the vibrating string.
One obvious route by which bow vibration might influence the bowed string relies on the cranked shape of a bow-tip (recall Fig. 2). Bending modes of the stick will naturally produce some rotation of this tip, and that will couple to longitudinal motion in the bow hair — bow hair is by no means rigid along its length. The time-varying friction force causing the string vibration is, of course, in the longitudinal direction along the bowhair, so (particularly when bowing near the tip) that friction force will be able to interact with stick vibration. But is this important? The effect would be confined to a frequency band close to each resonance. When players and bow-makers talk about the influence of a bow on the sound, they do not seem to be talking about note-specific effects (rather like the wolf note, discussed in section 9.4).
The physics of bow vibration has been explored in some detail by Colin Gough [3]. Many of the effects have been incorporated into a simulation model for a bowed string by Hossein Mansour [4]. But both authors only make very cautious statements about the possibility of a clear-cut influence of the bow on the sound of a violin. The physical effects they find seem very subtle.
But I don’t want to end this chapter on that negative note. We need to remind ourselves, yet again, that effects which are physically subtle can sometimes turn out to be perceptually significant to a musician. I will show some results about an effect that is not yet fully understood, but which seems to be connected with an aspect of bow vibration. I will put forward a speculative semi-explanation, arrived at in discussion with colleagues and friends Murray and Patsy Campbell.

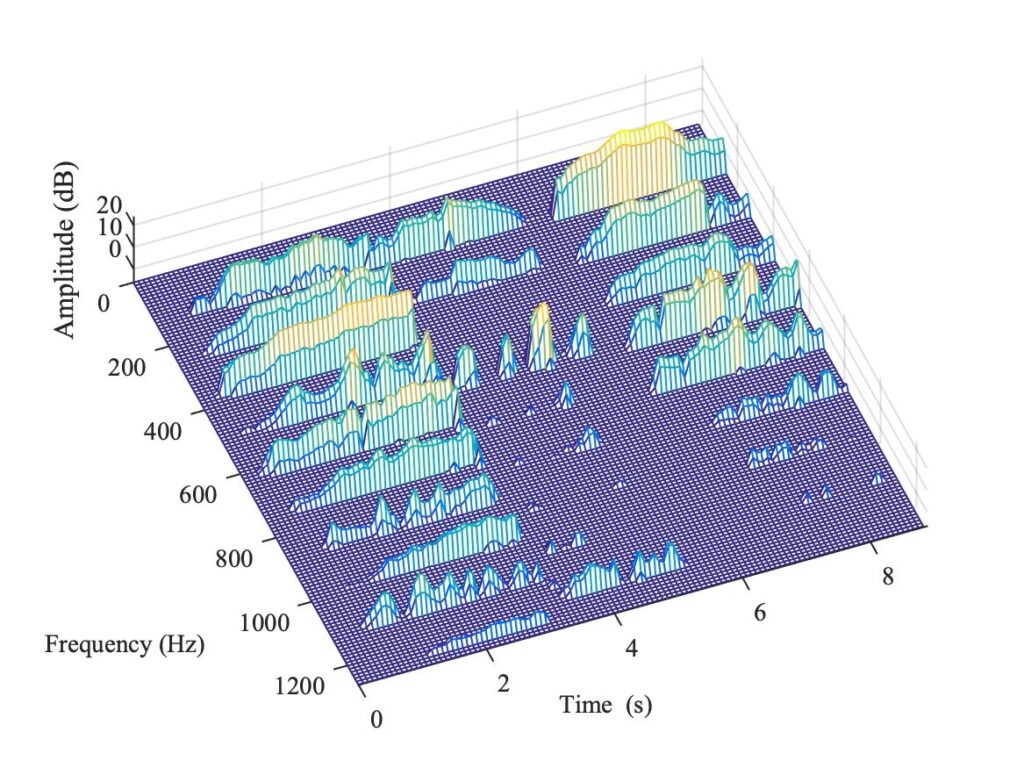
They are both multi-talented musicians, among other things being keen viol players (see Fig. 5). They pointed out a phenomenon that is sometimes heard in viols, and regarded as a nuisance by players. Listen to the three notes in Sound 1: they were all played on the same string of the viol, with nominally steady bow speed and force. In all three, perhaps most prominently in the middle note, you can hear a kind of “wah-wah” effect which we will call “warble”.
The effect is somewhat reminiscent of the cello wolf note, discussed in section 9.4. But the spectrogram shown in Fig. 6 shows that the effect is quite different from a wolf. A classic wolf note normally only affects a single note (near a strong body resonance), and it involves strong modulation in the fundamental frequency component as the Helmholtz motion alternates with double-slipping motion. Neither of those things is true for the viol warble. Figure 6 shows that for all three notes the fundamental, and the second and third harmonics, show little variation in time. The 4th harmonic, though, shows conspicuous and fairly regular modulation in all three notes, most prominently in the middle note. Some of the higher harmonics also show clear periodic modulation, not all with the same rate of repetition.
What is going on? Our tentative explanation involves transverse vibration of the bow-hair ribbon. A first step is to see that such transverse vibration can be excited by bowing, and can have audible consequences. We get rather clear evidence of that from a different test result. The viol bow seen in Fig. 5 was fitted with a small accelerometer, taped to the bow-hair near the frog so as to respond to transverse bow-hair vibration in the plane of the bow. The signal from this accelerometer was recorded simultaneously with two others: the output of a bridge-force sensor of the kind we have seen before, and the sound recorded by a microphone near the instrument body.
A recording was made of a bow change near the frog while bowing an open string on the viol: in other words, an up-bow followed by a down-bow. Figure 7 shows a spectrogram of the response from the accelerometer: you can hear the sound in Sound 2. The spectrogram shows vertical stripes marking the harmonics of the played note, but it also shows a prominent pattern of curving lines dotted out by bright spots on these vertical stripes. These lines mark the fundamental and the first few harmonics of a tone that rises in frequency as the bowed point approaches the frog, then falls again after the bow change. You can hear this rising then falling tone very clearly in Sound 2.
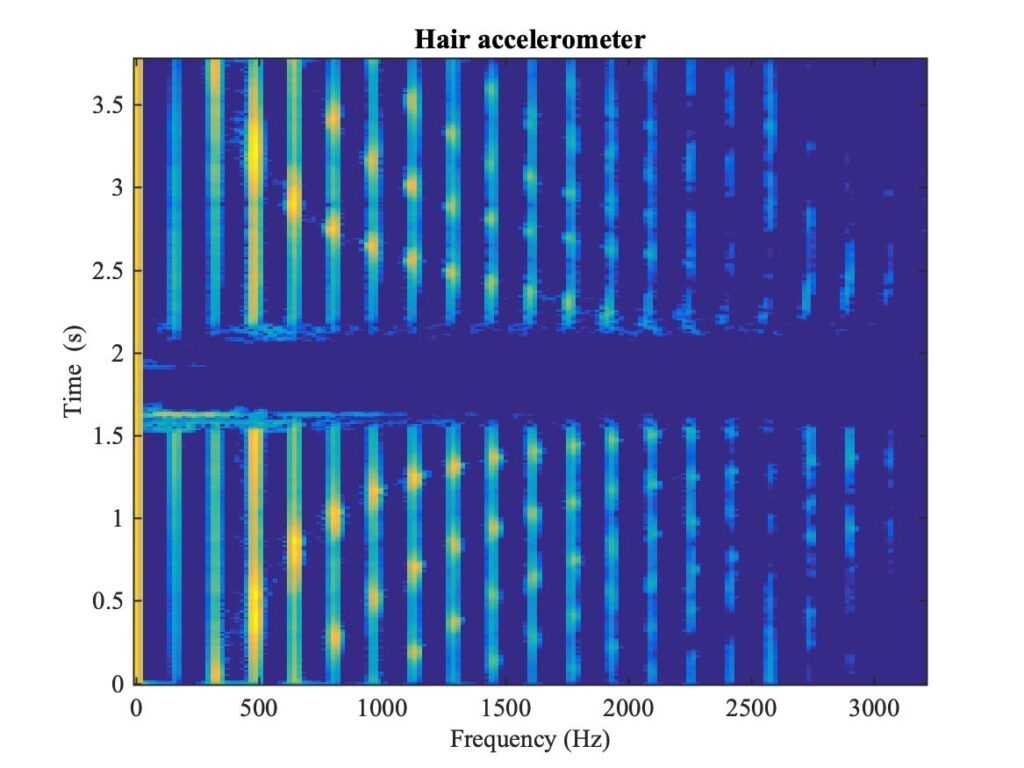
The rising-falling frequency you are hearing corresponds to the lowest resonance of the segment of bow-hair between the string and the frog: that segment gets shorter and then longer during the bow change, producing the rising and falling frequency. The bright spots in the spectrogram show that whenever one of the resonance frequencies of the short segment of bow-hair matches a harmonic of the played note, that bow-hair resonance is strongly excited. If we had placed another accelerometer near the tip, it would have picked up the corresponding vibration of the other segment of bow-hair: this would have produced a sound with the opposite trend, falling and then rising.
The rising-falling tone can be heard fairly clearly in the microphone recording, and seen in a corresponding spectrogram, but there is absolutely no trace of it in the bridge force recording. Putting these facts together, we learn three interesting things, none of them obvious. First, transverse bow-hair vibration is being strongly excited by bowing the string, despite the fact that the time-varying friction force is longitudinal in the bow-hair, approximately perpendicular to that transverse direction. Second, this bow-hair vibration is somehow creating radiated sound that can be picked up by a microphone and heard: but it is not doing this by influencing the usual transverse force at the bridge. Third, the fact that the bridge force seems unaffected suggests that the bow-hair vibration is having little influence on the stick-slip process of string vibration, the thing we have mainly been talking about throughout this chapter.
We can suggest a mechanism to explain the last two of these observations. Transverse vibration of the bow-hair will exert a force on the string at the bowed point, approximately perpendicular to the friction force. This can excite string vibration in that perpendicular direction. But remember that the bright spots in Fig. 7 always occur at harmonics of the played note, which will also be (approximately, at least) resonance frequencies of the string in the perpendicular direction, so this perpendicular string vibration might be quite strong.
Now think what happens at the bridge. The new perpendicular string vibration will not be detected by the bridge force sensor, because that is oriented to capture transverse vibration. But the perpendicular string vibration will exert a force on the bridge in that perpendicular direction, and so it can excite some body vibration (and thus create radiated sound). Possibly, the body response to such perpendicular forcing might be particularly strong in an instrument without a soundpost, as is the case for some of these early-pattern viols.
Returning to the viol warble, that too is not evident in a bridge force recording. This suggests that it might arise through a somewhat similar route, involving transverse vibration of the bow-hair and forcing at the bridge in the perpendicular direction. Support for this idea comes from a detail you can see in Fig. 5: notice that the bow stick has several white markers attached to it. These were empirically placed, to mark positions where the warble effect seemed most prominent. They form a suspiciously regular pattern, which corresponds to the nodal points of the 8th resonance of transverse hair vibration (count the segments between the markers).
Now, a nodal point of a mode of the entire length of bow-hair is also a point where both portions (to the left and right of the string contact) will resonate at the same frequency. So perhaps particularly strong perpendicular string vibration is excited when the bow is near these positions? Does this lie at the heart of the warble phenomenon? We don’t know for sure, yet. This proposed mechanism involves string vibration in two directions and bridge force in two directions, and gathering definitive data to see all those things simultaneously needs another round of instrumentation and data-gathering.
There is one more complication to mention: informal exploration of the warble effect suggests that it happens most strongly if the bow is not perpendicular to the string. Now, string teachers have always told pupils to avoid such “skewed” bowing. At least in the context of viol playing, perhaps avoiding warble is the main physical reason behind that advice?
[1] Anders Askenfelt and Knut Guettler, “The bouncing bow: an experimental study”, Catgut Acoustical Society Journal 3, 6, 3—8 (1998)
[2] Knut Guettler and Anders Askenfelt, “On the kinematics of spiccato and ricochet bowing”, Catgut Acoustical Society Journal 3, 6, 9—15 (1998)
[3] Colin E. Gough, “Violin bow vibrations”, Journal of the Acoustical Society of America 131, 4152–4163 (2012).
[4] Hossein Mansour, Jim Woodhouse and Gary P. Scavone, “Enhanced wave-based modelling of musical strings, Part 2 Bowed strings”; Acta Acustica united with Acustica, 102, 1094–1107 (2016).
