In the wider world of dynamics and acoustics, many different types of nonlinear phenomenon have been investigated. Over the centuries, musical instrument makers have exploited many of them in ingenious ways. These musical applications fall into two broad categories: modification by nonlinearity of sounds that have their origin in linear effects, and creation of sound by intrinsically nonlinear means.
The first category includes all the things we looked at in section 7.4: pitch glides and phantom partials in the harp, and additional brightness in the lute associated with a very slight buzz. A more drastic version of this last effect occurs in some Indian instruments like the sitar and tanpura: the immediately recognisable sound of those instruments is associated with a deliberately designed “buzzing bridge”. This category also includes instruments like the tamtam (Chinese gong): remember the spectrogram at the end of section 2.4 which was our first view of a nonlinear musical effect? Gongs and cymbals are set into vibration like most other percussion instruments by striking with some kind of drumstick or beater, but the sounds then take on the characteristic flavour of each particular instrument because of nonlinear effects.
The second category includes all musical instruments capable of producing a steady, sustained sound: the human voice, woodwind and brass instruments, bowed-string instruments, and also electronic instruments like the Theremin or Ondes Martenot, although we won’t have much to say about these. There are also musical effects which combine both categories: the sound of some nonlinear instruments can be modified by additional, independent nonlinearity. The trumpet and trombone give one example. As wind instruments, their sound production is intrinsically nonlinear (see chapter 11). But when a very loud note is played, the sound quality changes: the characteristic “brassy” sound. What is happening is that a shock wave is forming in the tube of the instrument (a sort of tame version of the sonic boom of a supersonic aeroplane). It changes the frequency content of the sound, in a somewhat similar way to the “clipping” phenomenon we met in the previous section.
In this section I will show some examples to give a first inkling of the diversity covered by the term “nonlinearity” — and also to give a clue why the words “linear” and “nonlinear” are used in this context. We can begin with something we understand, and have been using since Chapter 2: the ideal spring. Figure 1 shows a graph of the force in a spring, versus the displacement we impose by stretching or compressing it. If you pull on the spring, it pulls back with a force proportional to how far you have stretched it. If instead you push it, then it pushes back with a proportional force. The result is the straight line you see in the plot: it is surely very natural to describe this behaviour as “linear”, since it is captured by a single straight line.

The linearity in this case is associated with something called Hooke’s law, named after Robert Hooke. Hooke was a contemporary of Newton in the seventeenth century. He was involved in many things, from early microscopy to working with Sir Christopher Wren to survey and rebuild London after the great fire of 1666. He was the first to give a clear statement of the proportional relation between force and displacement in a spring. Not that his initial “publication” of the result was at all clear: he announced it in the form of an anagram, and only some years later revealed the unscrambled version!
But real springs are usually more complicated than this, especially if you try to stretch or compress them by a large amount. Instead of Hooke’s straight line, you may see a curve (and so “nonlinear” behaviour) like the ones plotted in red or blue in Fig. 2. These curves depart from the straight line in a rather well-behaved and progressive way. This is nonlinear behaviour in its most benign form: although, as we will see shortly, it can still be enough under some circumstances to induce striking nonlinear behaviour of a kind that no linear system can exhibit.
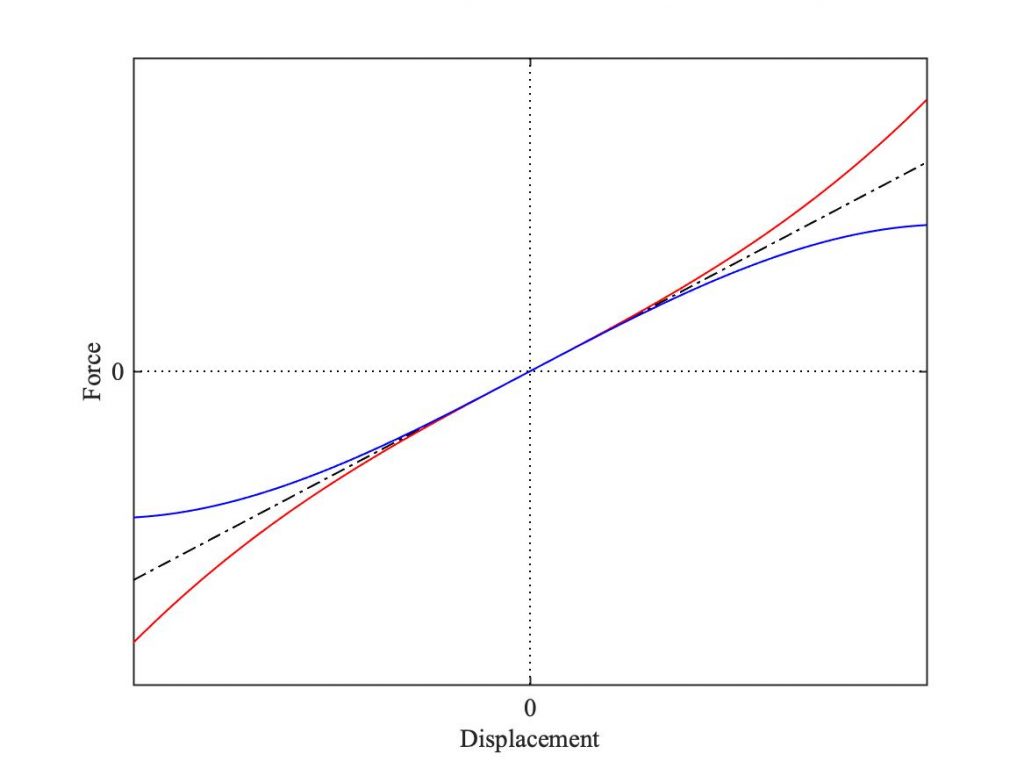
The red curve in Fig. 2 describes a hardening spring: the more you stretch it, the steeper the curve gets. The slope of the curve describes the stiffness of the spring: this kind of spring feels stiffer the more you stretch it. You can easily experience this effect with an ordinary rubber band: stretch one in your fingers, and when you try to pull it a long way it will feel much stiffer. (What is happening is that the spaghetti-like tangle of long-chain molecules in the rubber are being straightened out, so that it gets harder to stretch.)
It is easy to guess how an oscillator should behave if it has a hardening spring providing the restoring force: the oscillation will get faster when the amplitude is bigger. Shortly, we will look at a simple model to verify that this is indeed what happens. We have already met an example of a hardening-spring effect: the pitch glide that can happen at the start of a vigorously plucked note on a harp. The transverse vibration of the string increases the length a bit, and this increases the tension. Tension is the equivalent of the “spring” in a stretched string: it provides the restoring force, so the pitch of the note is higher when the amplitude is larger.
The blue curve in Fig. 2 shows the opposite kind of nonlinear behaviour: a softening spring. This time, when you pull the spring a long way, the stiffness gets lower rather than higher. An oscillator which includes a softening spring would be expected to vibrate at a lower frequency (in other words with a longer period) when the amplitude grows. We can see an example of this effect in a swinging pendulum. The “spring” in this case is provided by the force of gravity, tending to rotate the pendulum back towards the vertical position. When a pendulum swings with a small angle of displacement, it is approximately a linear oscillator. But when the angle of swing gets large, the strength of this gravity effect reduces. The details are described in the next link.
An extreme case happens if the pendulum swings so much that it almost reaches the vertical-upwards position before it starts to swing back down. It will “hesitate” in that position, because the gravity effect gets very small. Now think back to section 3.4, where we talked about church bell ringing in the British tradition. Bells are hung as pendulums, and bell-ringers take advantage of this softening-spring effect to give them a way to adjust the order in which the bells ring: by stopping the bell more or less near to the vertical position, they can make the swing period a little longer or a little shorter.
We can use a simple example problem to illustrate the behaviour of a mass-spring oscillator incorporating a spring that shows hardening or softening behaviour. Such an oscillator often obeys something called Duffing’s equation. This problem also illustrates the sense in which this kind of nonlinearity is “benign”. The key question is: can we find a suitable mathematical approach to allow at least some level of analysis and understanding of the nonlinear system? The detailed answer to that is explained in the next link, but the qualitative ideas and results can be described easily enough.
The approach illustrated in this link takes advantage of two kinds of approximation, both of which involve expressing something as a series expansion: a combination of terms that are convenient for mathematical analysis. The first of these is called a power series or Taylor series. We assume that we can express our slightly nonlinear function, as in Fig. 2, by adding to the linear behaviour of the force a bit of displacement squared, plus a bit of displacement cubed, and so on. Now the crucial approximation: if the nonlinearity is mild, we can hope that the successive terms in this series get rapidly smaller. (A mathematician would say “the series converges rapidly”.)
In that case we might get a good approximation to the behaviour by keeping only the first few terms, and disregarding the higher terms. For the kind of hardening or softening spring behaviour shown in Fig. 2, the response of the spring if it is compressed is a mirror image of the behaviour when it is stretched. What that means for our series expansion is that we don’t expect any squared term: the first nonlinear term is the cube of displacement. A squared term would produce hardening behaviour in tension, but softening behaviour in compression (or vice versa). So this gives us the recipe for Duffing’s equation: it describes an oscillator with a spring that behaves like a linear Hooke’s law spring, with the addition of a bit of displacement cubed.
To make some progress solving this equation, we now use another series expansion, one we have met before. We are interested in the behaviour of Duffing’s equation either when the oscillator is driven with a sinusoidal force, or the free motion when it is given some initial motion and then allowed to oscillate and gradually die away. In both case, the motion over any short interval of time would be expected to be periodic (or at least approximately so, in the case of the free decay). That means that we could express it as a Fourier series: a combination of sinusoidal terms at harmonically-related frequencies. Well, we can hope that this series will also converge rapidly, so that we might get a reasonable approximation by keeping just a few terms and ignoring the higher ones. The resulting approach is called the method of harmonic balance.
The result of applying the simplest version of harmonic balance to Duffing’s equation with a hardening spring is illustrated by a numerical example shown in Fig. 3. The details were explained in the previous link. The black curve shows the frequency response (on a dB scale) of the linear oscillator, ignoring the nonlinear term. The frequency scale shown here covers just a small range around the linear resonance frequency. Now we add the nonlinear term in, and we get the red curve. It leans over to the right. This is the effect of the hardening spring: as the amplitude grows, the apparent resonance frequency gets higher, just as we expected.
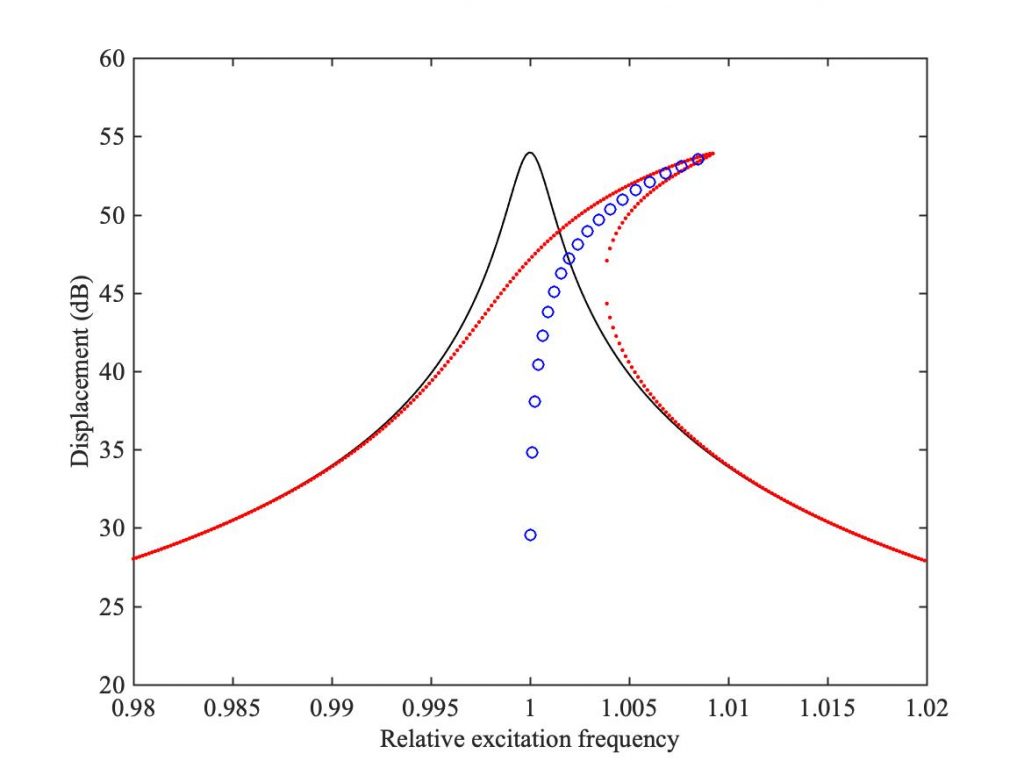
If you excite this oscillator at the peak, by the “nose” of the red curve, and then switch off the excitation so that the vibration gradually dies away, it will follow the line marked by the blue circles. As the amplitude reduces, the frequency moves back towards the linear resonance. This is the pitch-glide effect in action, just as we saw with the harp string in section 7.4.
The red curve has leaned over so far in this plot that there is a range of frequencies just above the linear resonance where there seem to be three different possibilities for the amplitude of the driven oscillator. How does it choose between these three? The answer is simple and quite intuitive, and is illustrated in Fig. 4. The system tries to continue what it is already doing, as long as it possibly can. So if you start excitation at a low frequency and then gradually increase it, the oscillator will follow the course suggested by the green arrows. As the frequency enters the ambiguous region, it simply carries on with what it was doing, following the upper branch of the curve. But when it reaches the “nose” of the leaned-over peak, it runs out of options. It is forced to jump down onto the lower branch, and continue along there as frequency continues to rise.

But if you start at a high frequency and slowly reduce it, something different happens, indicated by the blue arrows. This time when it enters the ambiguous region it continues along the lower branch. That is fine until it reaches the point where the curve turns vertical: when frequency falls below that value, the oscillator has to jump up the higher branch of the curve. This pattern of behaviour, with asymmetrical jumps and a hysteresis loop, is something that no linear system can do: a characteristically nonlinear phenomenon.
Figure 5 shows the corresponding behaviour to Fig. 3, but for a Duffing oscillator with a softening spring. This time the curve bends to the left, to lower frequency with increasing amplitude. This time if you start it at the nose of the red curve and then allow it to oscillate freely, you get an upward pitch glide as indicated by the blue circles.

Now look at Fig. 6, which repeats part of Fig. 2 with the addition of an extra line, in red dashes. This shows an extreme example of a hardening spring: it describes a linear spring with hard end-stops. If you try to stretch beyond an end-stop it is simply not possible: the force from the end-stop increases to match and counteract the force you are applying, without the spring stretching any further. This appears in the plot as a vertical line.

At first glance, this case may not look much more complicated than the hardening spring shown in the solid red line. But this comparison illustrates a distinction that is very important to the mathematicians: they would say that the solid red line is a smooth nonlinearity, but the dashed line is a non-smooth one. The sharp corner, followed by a curve that turns vertical, does not lend itself to the kind of power series expansion we used in the previous link to formulate Duffing’s equation. At a stroke, this removes some of the main tools for analysis, and mathematicians tend to regard non-smooth problems rather in the way that Transylvanians regard vampires: something to be avoided if at all possible.
Smooth nonlinearity offers at least the possibility of some kind of systematic approach to analysis, even if it needs to involve numerical computation as well. Non-smooth problems are not usually amenable to mathematical solution; there are some exceptions, but they tend to involve ad hoc ingenuity rather the application of systematic procedures. But the commonest approach to non-smooth problems is to make use of numerical simulation. That approach has the disadvantage that you can only compute a particular case. A mathematical solution, even an approximate one, can give insight into how the behaviour changes depending on the values of system parameters. To use numerical methods to gain similar information either involves exhaustive simulations of many cases covering a range of parameter values (a procedure sometimes referred to disparagingly as “carpet bombing”), or it involves ingenuity. We will meet examples of both carpet bombing and ingenuity when we look at the behaviour of bowed strings in Chapter 9.
What sources of nonlinearity tend to lead to smooth behaviour? We have already met examples of two important types. In earlier sections we have seen derivations of simplified linear governing equations for various vibrating systems: strings, bending beams, sound waves and so on. Every one of those derivations involved making assumptions that something was “small”, and using that as an excuse to ignore terms in a series expansion, to end up with a linear approximation. If instead you keep some or all of these terms, the system will be nonlinear in one way or another, but usually it will be smooth. When the “smallness” assumption concerned the displacement of the string or the beam, the result of relaxing the assumption is called geometric nonlinearity. On the other hand, when we illustrated the idea of a hardening nonlinear spring with the example of a rubber band, we were meeting material nonlinearity: a departure from Hooke’s law because of the way that a real material behaves. Again, such nonlinearities are usually smooth.
It is important not to think of smooth problems as being easy, or boring. It is emphatically not the case that “smooth means simple, non-smooth means complicated”. Rather, smooth means difficult and complicated, non-smooth means even more difficult and complicated. In fact, most of the well-studied examples at the core of “chaos theory” are based on smooth systems — precisely because it is easier to make mathematical progress with smooth problems. Even Duffing’s equation can show chaotic behaviour in some parameter regimes! In section 8.4 we will see some examples of chaotic response, and of sensitive dependence. Those examples will all be based on remarkably simple systems.
Figure 7 shows another possible kind of non-smooth nonlinear behaviour. This describes, in idealised form, the response of a linear spring connected to the applied force by something with a bit of play in it — a loose bolt, for example. The phenomenon captured here is sometimes called backlash, or sometimes a dead band: a flat portion in the centre of the plot. This is the range of displacements covering the free play in the loose bolt. No force at all is exerted while we are within this region. But then the bolt makes contact with the spring, and the linear spring behaviour starts.

Force-displacement relations in nonlinear springs are not the only thing we can represent with curves like these. Figure 8 relates to the idea of hard and soft clipping, discussed in section 8.1. The red curve shows the input-output relation of an amplifier showing hard clipping. The response is linear until the limit is reached, then it turns over abruptly into a horizontal line because the output can never exceed the limiting level. The blue curve illustrates the soft clipping effect: the curve has a generally similar shape to the red curve, but without the sharp corners. The blue curve is a smooth nonlinearity, but the red curve is non-smooth. This pair of curves also serves to illustrate one way that a mathematician might approach a non-smooth problem: they may try to replace the non-smooth problem (red curve) by a smooth one which approximates it (the blue curve). The jargon term for this sort of replacement is regularisation.

There is another important nonlinear phenomenon that can be described through a plot: friction. Picture a coffee mug sitting on a table. Now get hold of one edge of table, and lift it so that the table tilts. If you tilt far enough, the mug will start to slide down the table. What you are seeing is the transition between sticking friction and sliding friction. With a gentle tilt angle, the friction force between the mug and the table is enough to hold it still, but beyond a critical angle there isn’t enough friction, and the mug slides.
The simplest idealisation of this behaviour comes from some empirical “laws” associated with two French scientists from the 17th and 18th centuries: Guillaume Amontons and Charles-Augustin de Coulomb. We will have more to say about this subject in Chapter 9 when we delve into the mechanics of a bowed string. For now, it is enough to see two pictures.
Figure 9 shows the simplest case. The quantity along the horizontal axis this time is the sliding speed between the two objects, such as the mug and the table. The red zig-zag curve shows the behaviour of the friction force. When the sliding speed is zero, the mug is not sliding. The friction force can take any value between two limits, indicated by the vertical portion of the curve. In the tilting table experiment, the friction force will adjust itself to be just big enough to prevent sliding with a given tilt angle. But once the mug is sliding, there is a friction force which is either positive or negative depending on the direction of sliding: friction always opposes the sliding motion. These are the two horizontal segments of the curve.

However, this model is wildly over-simplified. We can improve it a little, while still using the pictorial approach. If the friction force between two objects is measured at different sliding speeds, it usually doesn’t show the horizontal lines suggested by Coulomb, as plotted in Fig. 9. Instead, for many surfaces (including violin rosin, which will be of particular interest to us later) the behaviour looks more like the plot in Fig. 10. When sliding is very slow, the friction force can be quite large, but with faster sliding the force is lower.

Both these models of friction give rise to non-smooth behaviour: curves with sharp corners and vertical portions. In the light of the comments made earlier, we don’t hold out much hope for easy mathematical solutions to problems involving vibration driven by friction, whether it is a violin bow and a string, or a wet finger round the rim of a wineglass. But this is where ingenuity can come in: we will meet examples in later sections, but we can show one simple example now to illustrate how vibration involving friction can give unexpected patterns.
This example describes a friction damper. Picture a mass-spring oscillator, with the mass resting on a table where Coulomb friction (as in Fig. 9) operates. You pull the mass sideways and stretch the spring, then let go. If you have pulled it far enough that the spring force exceeds the limit of sticking friction, the mass will slide back. The first time the speed comes back to zero is after half a cycle of vibration. At that point, one of two things will happen. If the spring force isn’t enough to exceed the limit of friction, the mass simply stays put, sticking to the table. But if the spring force is enough to exceed the limit of friction in the opposite direction, the mass will slide back and perform another half-cycle of vibration. This process then repeats. Every time the mass slides, energy is lost against the friction force, so the amplitude decreases every half-cycle. Eventually, the mass will come to rest because the spring force is no longer big enough to exceed the limit of friction.
An example of the resulting waveform of displacement of the mass is shown in Fig. 11. The details behind the calculation are described in the next link. The most striking thing about this waveform is that the decay envelope is a straight line, rather than the exponential decay associated with linear vibration of any kind. This form of decay envelope is a diagnostic feature of friction dampers. If an envelope like this is seen in a measurement, it tells you that friction is probably playing a big part in the dissipation of energy: a useful clue for identifying the essential physics governing the vibration.

