A familiar example of an oscillator showing weakening-spring behaviour is a pendulum, like the sketch in Fig. 1. A mass $m$ is suspended from a rigid, massless rod of length $L$. The rod is pivoted at the other end, with no friction.
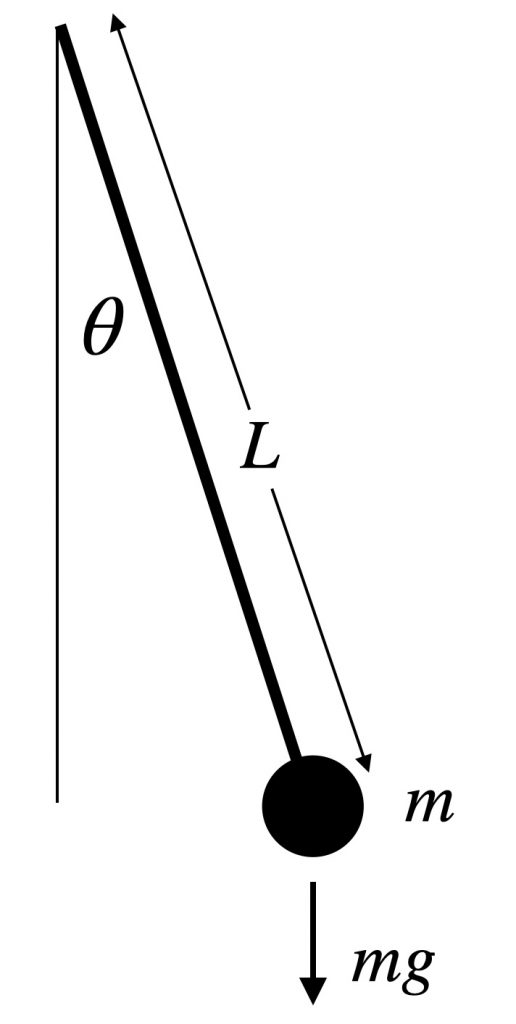
The only external force acting on the mass is gravity, so taking moments about the pivot we obtain
$$m L^2 \ddot{\theta} = -mgL \sin \theta .$$
We can rewrite this to look like the equation of an equivalent mass-spring oscillator:
$$m \ddot{\theta} + \dfrac{mg}{L} \sin \theta =0 ,$$
so that the equivalent “nonlinear spring” has the force-“displacement” relation $(mg/L) \sin \theta$.
This spring characteristic is plotted in Fig. 2, in a form that can be compared with Fig. 2 of Section 8.2 for hardening and softening springs. The plot only shows values $-\pi \le \theta \le \pi$ because we are interested in cases where the pendulum oscillates backwards and forwards, rather than rotating all the way round. We will be interested in the rotating case later, though: we return to it in Section 8.3.

It is clear that the pendulum shows softening behaviour. We can link the behaviour explicitly to the earlier plot and to Duffing’s equation (see section 8.2.2) by using the power-series expansion of $\sin \theta$ for small angles:
$$\sin \theta \approx \theta – \dfrac{\theta^3}{3!} .$$
Our equivalent spring follows Hooke’s law for very small displacements $\theta$, and then the first departure from linear behaviour takes the form of a cubic term with a negative coefficient. For larger angles $\theta$, Fig. 2 shows that the spring force reaches its maximum value at $\theta = \pi/2$ when the pendulum is horizontal, and then it falls all the way to zero as the angle approaches $\pi$, with the pendulum vertically upwards.
